copyright © 1995 Vance Gloster Last Modified: Oct 8, 1995
This lesson originally appeared on StickWire - the Official Chapman Stick Mailing List.
Reproduced here by permission. This article can be reprinted only in its entirety.

Theory On Tap
Lesson 5: The Circle of Fifths




 Copyleft 1995 Vance Gloster

[This document is licensed using the GNU copyleft license. That means anyone can make a copy of this work. No one can sell a copy of this work (they can charge a small copying fee for providing a copy). Anyone can modify this work but they must make the resulting work available under the same terms. It cannot be included in a work (such as a book or magazine) that is sold without permission which is usually granted in exchange for a license fee.]


I. The Concept

Lots of fields have some device that is used to illustrate concepts which would be difficult to understand without it. A case in point is the Moebius strip for mathematicians. This Moebius strip has only one side and one edge despite being a 3-dimensional figure. It illustrates some of the central concepts of Topology, a field of mathematics that studies properties of physical shapes. Other fields have similar symbols. Shipboard navigators had their sextants for sighting stars, and engineers their sliderules.

In music, the Circle of Fifths plays a similar role. The Stick makes good use of many of the relationships that the Circle of Fifths illustrates, so it is especially important and relevant to Stick players.


II. The Circle

The entire name of the Circle is "The Circle of Fifths and Fourths". This is normally abbreviated to just The Circle of Fifths and in its most basic form it looks like this:



Click to see Vance's original

As you go clockwise each successive note is a fifth above the previous note. As you go counter-clockwise (or anticlockwise for any UK residents) each note is a fifth below the previous note. So where do fourths come into it? It is also true that as you go clockwise each note is a fourth down from the previous note, and as you go counter-clockwise each note is a fourth above the previous note.

The internal relationship that makes this possible is the fact that going up a fifth and down a fourth brings you to the same letter note (though in a different octave). For instance going up a fifth from C brings you to a G and going down a fourth from the same C brings you also to G, but an octave down.

This particular trick is the basis of many of the interesting properties of the tuning system of the Stick. The treble strings are in fourths while the bass strings are in fifths and in reverse order. This allows the same chord shapes to be played on both sides, though they will result in different inversions.


III. Major Keys

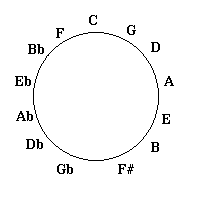
The circle of fifths can also be used as a guide to figuring out how many flats or sharps a particular key has. If you start at C and move counterclockwise, each successive key has one more flat in its key signature than the previous one. If you start at C and move clockwise, each successive key has one more sharp than the previous one. This means we can write the circle thus to show key signatures.



Click to see Vance's original

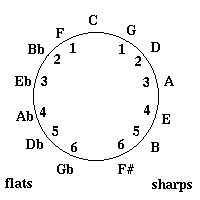
As you can see the key of A has 3 sharps, and the key of Db has 5 flats. But which notes are the flats and sharps? If you start at Bb and move counterclockwise you will get the flats in order. For instance in the key of Db the flats in the key signature are Bb, Eb, Ab, Db, and Gb. If you start at F (which is right next to Bb, the starting point for the flats) and move clockwise you will get the sharps in order. For instance the sharps in the key of A are F#, C#, and G#.


IV. Minor Keys

So do we need a different circle of fifths to do the same thing for minor keys? No, this one works just fine. The difference is that A minor has no flats or sharps, so we need to rotate the outer circle three notches counter-clockwise. The resulting circle looks like this:



Click to see Vance's original

The order of the flats and sharps is done exactly like major keys.


V. Modes

Similarly to how we rotated the outer circle to change from major keys (Ionian mode) to minor keys (Aeolian mode), one can do the same thing for the other modes. Here is the information about how many steps and the direction of rotation for all the modes from the normal major position.

Mode Number of steps Direction
Ionian 0
Dorian 2 Counter-clockwise
Phrygian 4 Counter-clockwise
Lydian 1 Clockwise
Mixolydian 1 Counter-clockwise
Aeolian 3 Counter-clockwise
Locrian 5 Counter-clockwise

VI. Consonance vs. Dissonance

The circle also expresses whether a particular key change or chord change will sound "smooth" (consonant) or "jarring" (dissonant) or somewhere in between. The rule is that closer the two keys or chords are on the circle, the more consonant it will sound. For example, if you are playing in the key of C, the smoothest modulation is to move to either F or G. The "whole step up" modulation that became a cliche in pop music earlier in the century is a little more jarring, but still pretty consonant being just one step further away on the circle (C to D for instance).

Looking at the circle as representing chords, it is no accident that the I, IV, and V chords of any key are adjacent (for instance C, F, and G in the key of C) because these chords provide very consonant progressions. On the other hand, moving 6 positions in either direction provides a jump of a tritone (diminished fifth) which is the most dissonant interval, key change, or chord change.

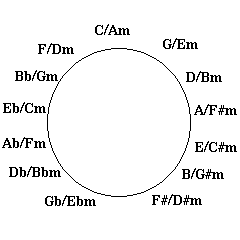
When analyzing real songs that include both major and minor chords it is most useful to use a circle which has a major chord and the relative minor at each position. It looks like this:



Click to see Vance's original

As you can see from this circle, very consonant songs like "Heart and Soul" (C-Am-F-G) use a limited area of the circle (three positions) while slightly more adventurous progressions like the Who's "I'm Free" (C-F-G-D-G-A) use more area (five positions).

The proximity on the circle can also be used in a simplistic chord substitution strategy. If you want a substitute chord for C in a progression, the ones close to it on the circle will make reasonable substitutes. Jazz theory teaches more involved chord substitution approaches involving analysis of the progression, but this method can get you started with it.


VII. Why a Circle and not a Line of Fifths?

So far we have spread the points around a circle, but it is not clear why it should be a circle. One reason is that in a chromatic scale there are only 12 possible notes (ignoring octaves). This implies that if we make the circle a line, it will have to repeat itself a lot as it streches toward infinity. On the other hand, there are almost an unlimited number of ways to "spell" a particular note. For instance C can be written as C, Dbb, Ebbbb, B#, A###, etc. Other notes are commonly spelled two different ways (such as G# which is the same note as Ab). So let us look at yet another circle of fifths that allows each chromatic note a position, but which the different "spellings" of that note share.



Click to see the original

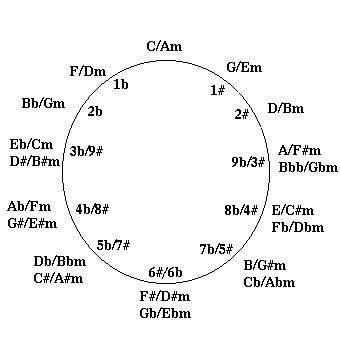
The real reason we need the circle is so we can see the relationships that go "around the back" of the circle. If you were reading a piece of music and the key changed from Db (five flats) to F# (six sharps), you would think that the effect would be jarring. But on the new improved circle we can see that this is quite consonant because the positions are adjacent. The only thing that is jarring is the change in spelling, and if the musician is doing his or her job this is not audible.


VIII. Stick-specific Applications of the Circle

First is how to figure out the tuning on one side of a Stick if you know one note (this assumes one of the standard fourths on melody and fifths on bass tunings). Find the note you know on the circle and the strings will be listed around the circle. For instance if you know that the lowest melody string on a standard-tuned Stick is a C#, you can read the tunings of the strings (left-to-right on the Stick) by reading counter-clockwise on the circle starting at C#.

This technique can also be used to figure out what the result will be if you move a note or chord over by one string. Moving to the right corresponds to moving counter-clockwise on the circle. Moving to the left corresponds to moving clockwise on the circle.

Next moving up by one fret dot on the Stick is moving up a fourth. This corresponds to shifting one position counter-clockwise on the circle. For instance, if you are playing a C (note or chord) and you move it up the neck by one fret dot, the result will be F, one position counter-clockwise from C on the circle. Similarly moving down the neck by one fret dot is equivalent to moving one position clockwise on the circle.

This can also be used to figure out how to transpose a song into a different key. Let us say that you want to transpose from C to Eb. Eb is 3 positions counter-clockwise from C on the circle. One approach which does not involve using the circle is to shift your hand up 4 frets (the interval between Eb and C). But another approach is to move to the right by 3 strings. You can substitute moving up the neck by one fret dot for moving over a string, so you could also move up one fret dot and over 2 strings.


IX. Conclusion

The circle is a valuable tool that helps you to see the fundamental relationships that music, and especially the Stick are based upon. Spending time with it will usually result in a better understanding of these relationships that can help both your playing and your composition skills.

Lessons: 1| 2| 3 - Part I| 3 - Part II| 4 - Part I| 4 - Part II| 5| 6| 7| 8| 9| 10| 11| 12|
Copyleft 1995 Vance Gloster
Page maintained by Me